The softmax function is a cornerstone of machine learning, especially in tasks involving classification. It transforms raw prediction scores (logits) into probabilities, making them easy to interpret and use for decision-making. This blog post will dive deep into what the softmax function is, why it’s important, and how to effectively implement it using Python and PyTorch.
Table of contents
What is the Softmax Function?
The softmax function is used in machine learning, particularly in classification tasks, to normalize the outputs of a network into probabilities. It ensures the outputs sum to 1, thereby turning raw numbers into interpretable probabilities. Formally, the softmax function is defined as:
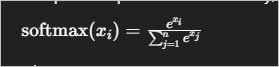
where:
- xix_i is the input score for class ii.
- ee is the exponential function.
- nn is the total number of classes.
Why is Softmax Important?
Softmax is crucial because it simplifies complex outputs into a probabilistic format that clearly indicates the likelihood of each possible class. This is particularly valuable in multi-class classification scenarios where decisions are based on the highest probability.
Consider an image classification task: a model predicting whether an image is a dog, cat, or bird. Raw scores like [3.2, 5.1, 2.7] do not clearly indicate probabilities. Applying softmax converts these scores into probabilities, such as [0.17, 0.75, 0.08], making it clear that the model is most confident that the image depicts a cat.
Mathematical Insight
The softmax function enhances the scores by amplifying differences. Scores with higher values become much more significant after exponentiation, while lower scores shrink considerably. This emphasis helps the model clearly differentiate between classes.
Implementation in Python
Here’s a simple implementation of the softmax function using Python and NumPy:
import numpy as np
def softmax(x):
e_x = np.exp(x - np.max(x))
return e_x / e_x.sum()
# Example usage
scores = np.array([3.2, 5.1, 2.7])
probabilities = softmax(scores)
print(probabilities)
This snippet outputs normalized probabilities:
[0.16984696 0.75446768 0.07568536]
The highest probability clearly identifies the predicted class.
Using Softmax in PyTorch
PyTorch, a popular deep learning library, simplifies softmax computation through its built-in functionalities. Here’s how you can implement softmax using PyTorch:
import torch
import torch.nn.functional as F
# Example scores (logits)
scores = torch.tensor([3.2, 5.1, 2.7])
# Applying softmax
probabilities = F.softmax(scores, dim=0)
print(probabilities)
Output:
tensor([0.1698, 0.7545, 0.0757])
PyTorch’s built-in function ensures numerical stability and efficiency, essential in deep learning.
Softmax in Neural Networks
In neural networks, softmax typically serves as the activation function in the final layer of a classification model. Let’s illustrate this with a basic neural network in PyTorch:
import torch
import torch.nn as nn
import torch.nn.functional as F
class SimpleClassifier(nn.Module):
def __init__(self, input_dim, output_dim):
super(SimpleClassifier, self).__init__()
self.fc = nn.Linear(input_dim, output_dim)
def forward(self, x):
logits = self.fc(x)
probabilities = F.softmax(logits, dim=1)
return probabilities
# Create model
model = SimpleClassifier(input_dim=10, output_dim=3)
# Example input
input_data = torch.randn(1, 10)
output_probabilities = model(input_data)
print(output_probabilities)
This will output something similar to:
tensor([[0.2571, 0.6154, 0.1275]], grad_fn=<SoftmaxBackward0>)Tools and Best Practices
Several tools enhance the usage of softmax in AI development:
- PyTorch: Offers intuitive and efficient implementations for softmax, particularly useful in deep learning models.
- TensorFlow: Provides similar functionalities with easy integration into complex neural network architectures.
- NumPy: Ideal for understanding and prototyping softmax in simpler computational scenarios.
When using softmax, it is crucial to consider numerical stability. Always subtract the maximum value from scores before exponentiation to prevent overflow issues, a practice naturally handled by PyTorch and TensorFlow.
Softmax vs. Sigmoid
It’s important to distinguish softmax from sigmoid, another activation function:
- Sigmoid is typically used for binary classification tasks, providing a probability between 0 and 1 for each class independently.
- Softmax handles multi-class scenarios, ensuring that all class probabilities sum up to 1, making it perfect for tasks with mutually exclusive classes.
Practical Applications
Softmax is extensively used in:
- Image Classification: Models like ResNet and MobileNet use softmax to classify images into distinct categories.
- Natural Language Processing (NLP): Transformer-based models (like BERT and GPT) rely on softmax to predict the next word or classify text.
- Recommender Systems: Softmax can also aid in predicting user preferences and providing recommendations based on probability distributions.
Conclusion
The softmax function is an indispensable tool in AI, particularly within the context of multi-class classification problems. It translates ambiguous model outputs into meaningful probabilities, enhancing interpretability and decision-making clarity. Leveraging powerful libraries like PyTorch simplifies implementation, allowing developers and data scientists to build robust, effective models with ease.
Discover more from CPI Consulting -Specialist Azure Consultancy
Subscribe to get the latest posts sent to your email.